4.6 High Curie Temperature NdFeCoGaB Permanent Magnetic Alloy: Development and Performance
To improve low Curie temperature, coercivity and bad thermal stability of ternary alloy \(Nd_{15}Fe_{78}Co_{8}B_{7}\), using Co and Ga to replace part of iron to constitute variation order and effect of element dynamic cross of quinary alloy.
Preparation Process and Experimental Methods for NdFeCoGaB Alloys
Sample was prepared as per \(Nd_{16}(Fe_{1 - x}Co_{x})_{77}B_{7}\), where \(x = 0\), 0.05, 0.1, 0.2, 0.3. Samples with Ga was prepared as per \(Nd_{16}Co_{0.16}Fe_{61 - x}Ga_{x}B_{7}\), where \(x = 0\), 1, 2, 4, 7. Prepared material was melted in vacuum non - consumable arc furnace with argon protection. Melted material was crushed roughly in crushing appliance, and pulverized to 3.5 μm, and then the powder was molded under magnetic field of 1.5T and pressure of 2T/cm². Molded roughcast was sintered in furnace at 1100°C for 1 hour and edged at 600°C, and then quenched to room temperature. Samples of good sintered and edged were magnetized in strong pulse magnetic field. Magnetic parameters were measured using CL - 6 magnetic measurer and Curie temperature was measured by magnetic balance.
Condition for X - ray diffraction experiment: copper target with wave length 0.15418nm. The Mössbauer spectrum was measured under iso - accelerating the Mössbauer spectrum. Experiment was carried out at room temperature, radiation source was 57Co (Rh) and used \(\alpha - Fe\) for measure velocity and took the central route as zero point of velocity. All Mössbauer experiment sample were in state of powder. All Mössbauer spectrum used a group of single-line spectrum, a group of dual-line spectrum and 6 groups of hexed-line spectrum to fit by the least square method, and six inequivalent iron crystal sites corresponding to Nd-rich phase and B-rich phase and tetragonal phase (Pan, 1986; Ping, Li, Ma, Pan, et al, 1986; Ma, et al, 1984).
Enhancing Curie Temperature by Replacing Iron with Cobalt in NdFeCoB Magnets
Table 4.1 is the result of magnetism and Curie temperature measurement for sample of \(Nd_{1.6}(Fe_{1 - x}Co_{x})_{77}B_{7}\), with different cobalt contents. It can be seen from Table 4.1 that Curie temperature was heightened with increasing cobalt content, but the coercivity (\(_{j}H_{c}\)) and remanence (\(B_{r}\)) declined with increasing cobalt, thus magnetic energy product \((BH)_{max}\) was also declined.
There are 6 inequivalent iron sites in \(Nd_{2}Fe_{14}B\), Curie temperature is raised with increase of atomic distance of Fe-Fe. Among 6 sites \(j_{1}\) and \(j_{2}\) have most important function on Curie temperature. At first \(j_{2}\) has the most neighboring atoms (12) and its distance with the neighboring atoms is the biggest (\(268\times10^{-12}\ m\)) so that it has the strongest exchange function. The next iron atomic distance be - tween \(j_{1}\) site and \(k_{2}\) and \(j_{1}\) site are \(2.936\times10^{-13}\ m\) and \(2.433\times10^{-13}\ m\), respectively, that are smaller than critical distance \(245\times10^{-12}\ m\) of plus minus exchange integral. When cobalt content \(x > 0.2\) cobalt atoms occupies \(j_{2}\) site preferentially (Ping, Li, Ma, Pan, et al, 1986), the minus exchange function is improved because exchange integral \(j_{Co - Co}>j_{Co - Fe}>j_{Fe - Fe}\). Simultaneously, when \(x < 0.2\) Co atom occupies \(j_{2}\) site preferentially, which will further increase function of plus exchange. The re - sult leads to increase of Curie temperature with increase of cobalt content. Site \(j_{2}\) has a strong plane anisotropy, thus the preferential replacement of cobalt atoms will enhance plane anisotropy, but hypolattice anisotropy of neodymium is bigger than that of 3d transit metals so that increase of cobalt content decreases single axis anisotropy of tetragonal phase \(Nd_{2}(Fe_{1 - x}Co_{x})_{14}B\), but in whole range of re - placement by cobalt the tetragonal phase is still axial anisotropy. In addition, along with increase of cobalt magnetic soft phase Nd(Co, Fe)2 appeared and it may form nucleation point in process of reverse magnetization. Therefore, coer - civity of the alloy degrades rapidly with increase of cobalt content. In preparation of samples it is necessary to control condition of process to avoid appearance of \(Nd(Co, Fe)_{2}\) phase to enhance the coercivity.
Effects of Gallium Substitution for Iron in NdFeCoB Permanent Magnet
Table 4.4 is measuring result of magnetism and Curie temperature of \(Nd_{1.6}Co_{0.16}\)
\(Fe_{61 - x}Ga_{x}B_{7}\). It can be seen that Curie temperature declines fast with increase of \(x\) when \(x < 2\), and Curie temperature declines slowly when \(x > 2\). Author used Mössbauer method to study this phenomenon.
As described in section 4.6.2 \(Nd_{2}Fe_{14}B\) tetragonal phase had 6 inequivalent iron sites, when Co and Ga are added they will occupy some of the sites and their occupation probability is:
\(\begin{cases} P_{Fe}^{i}=[C_{Fe}/(C_{Fe} + C_{Co})]\times[S_{i}/\sum_{i = 1}^{6}S_{i}]\times\frac{14}{n^{i}}\\ P_{Co}^{i}=\beta^{i}P_{Fe}^{i}\\ P_{Ga}^{i}=1 - P_{Fe}^{i}-P_{Co}^{i} \text{ (Compiling Group, 1979)} \end{cases}\) (4.6)
where \(P_{Fe}^{i}\), \(P_{Co}^{i}\) and \(P_{Ga}^{i}\) present probability to occupy the site No. \(i\) respectively; \(C_{Fe}\), \(C_{Co}\) and \(C_{Ga}\) present iron and cobalt content in the alloy, respectively; \(S_{i}\) is the area parameter in the Mössbauer fitting; value \(n^{i}\) (\(i = 1 - 6\), represent sites \(j_{2}\), \(k_{2}\), \(j_{1}\), \(k_{1}\), \(e\) and \(c\)) is decided by formula below:
\(n^{j_{2}}:n^{k_{2}}:n^{j_{1}}:n^{k_{1}}:n^{e}:n^{c}=2:4:2:4:1:1\) (4.7)
where \(\beta^{i}\) is the atomic rate of iron to cobalt when gallium content is 0 and is a constant relative to a certain site.
By Eq.4.6 and Eq.4.7 and the Mössbauer fitting result that the curve of gallium atom occupation probability changes with change in gallium content \(x\) is obtained as shown in Fig. 4.24. The broken line represents random distribution status
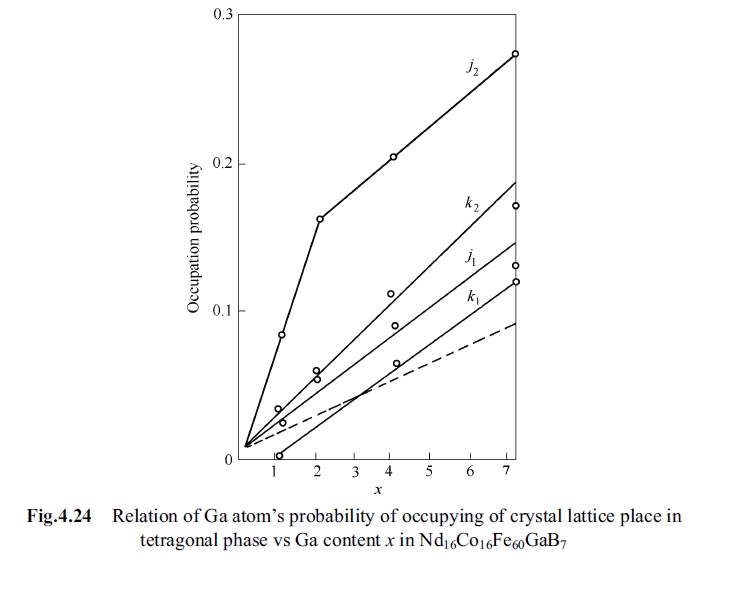
of gallium in each site. It was obtained by calculation that the occupation probability of sites \(e\) and \(c\) is minus, almost be zero that indicated gallium does not occupy that two sites.
It is obviously that when \(x\leq2\) gallium mainly occupies site \(j_{2}\), when \(x > 2\) gallium has a certain probability to occupy each site of \(k_{2}\), \(j_{1}\) and \(k_{1}\) yet. The very interesting thing is that at position \(x = 2\) occupation probability curve of gallium in site \(j_{2}\) presents slope variation. Exchange function of \(j_{2}\) site is positive, and exchange function of \(j_{1}\) and \(k_{2}\) sites is negative. When gallium occupies \(j_{2}\) site preferentially Curie temperature declines quickly with increase of gallium content when \(x\leq2\) because positive exchange function is replaced by zero exchange function. Also when \(x > 2\) for sites \(j_{1}\) and \(k_{2}\) the part of negative exchange function is replaced by zero exchange function, that is in favor of raising of Curie temperature. But generally, the probability to occupy \(j_{2}\) site by gallium is bigger than that to occupy other sites thus Curie temperature still declines when \(x > 2\), and only it declines slowly compared with that when \(x\leq2\). Therefore, using the Mössbauer method can well explain the variation tendency of the Curie temperature with change of gallium content.
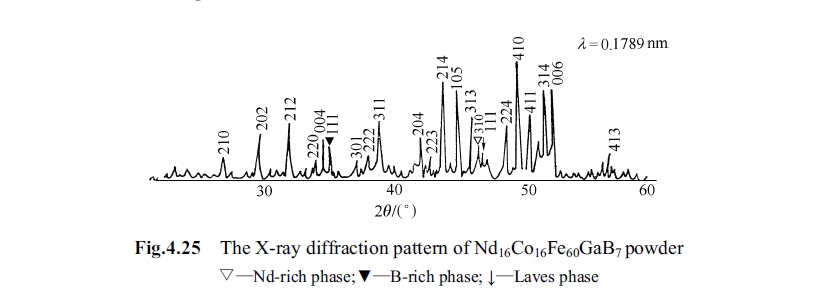
Experiment result of X - ray diffraction indicates that X - ray diffraction patterns of 5 alloys with different composition are similar, the different is just some perks have some displacement. Fig. 4.25 shows the X - ray diffraction pattern when \(x = 1\). It can be seen from the figure that Laves phase exists after adding gallium, which limits further enhancement of coercivity. Experiment result indicates that when \(x\) is increased from 4 to 7 X - ray diffraction peak offsets to direction of small angle, that indicates gallium enters into crystal lattice and lattice parameters \(a\) and \(c\) vary with increase of gallium content, the relative data is shown in Table 4.11.
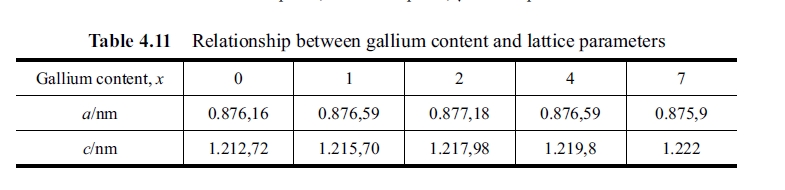
It can be seen from these data that lattice constant \(a\) of the quadrilateral phase increases with increase of gallium content at beginning and reaches the maximum when \(x = 2\); if \(x > 2\) the constant decreases gradually; but lattice constant \(c\) increases with increase of gallium content.
It can be known from above analysis that for \(Nd_{16}Co_{16}Fe_{61 - x}Ga_{x}B_{7}\) gallium can enter into the quadrilateral phase and coercivity reaches the highest when \(x = 2\).
\(Nd_{16}Co_{16}Fe_{61 - x}Ga_{x}B_{7}\) was edged at 580°C for 3 h and then quenched to room temperature and prepared to film for electronic microscope as per procedures mentioned in section 2.3.2 of this book. Variation in crystal interface and interior of crystal was observed under electronic microscope. Three points were found as follows:
- Crystal interface was flat and straight after edging, seeing Fig. 4.26 and Fig. 4.27.


- Ga - rich phase (\(Ga_{2}Nd\)) enters into the matrix phase \(Nd_{2}Fe_{14}B\) and the figure of Ga - rich phase appears in the matrix phase as shown in Fig. 4.28 to Fig. 4.30. Its microstructure looks like a trip in the matrix phase, indicating that the Ga - rich phase and \(Nd_{2}(Fe, Ga)_{14}B\), \(Nd_{2}(Fe, Ga)_{14}B\) and \(Nd_{2}Fe_{14}B\) are in deep coherence.
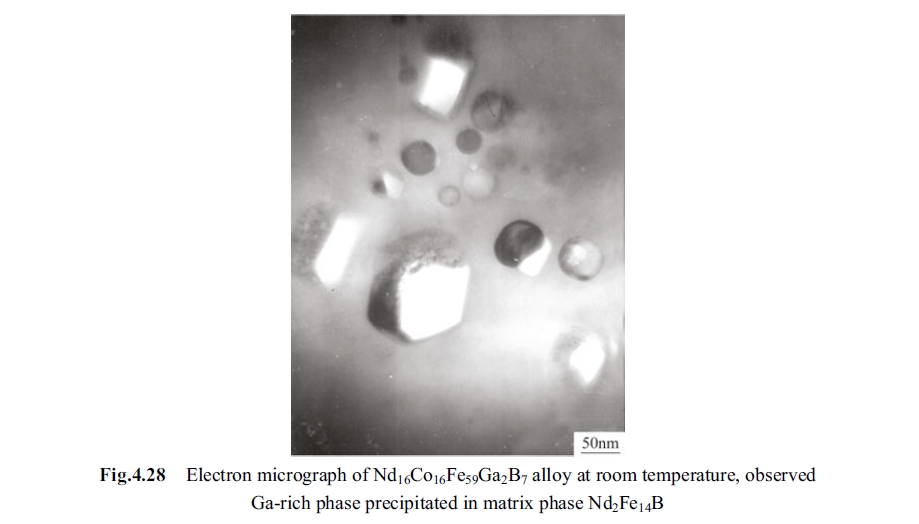
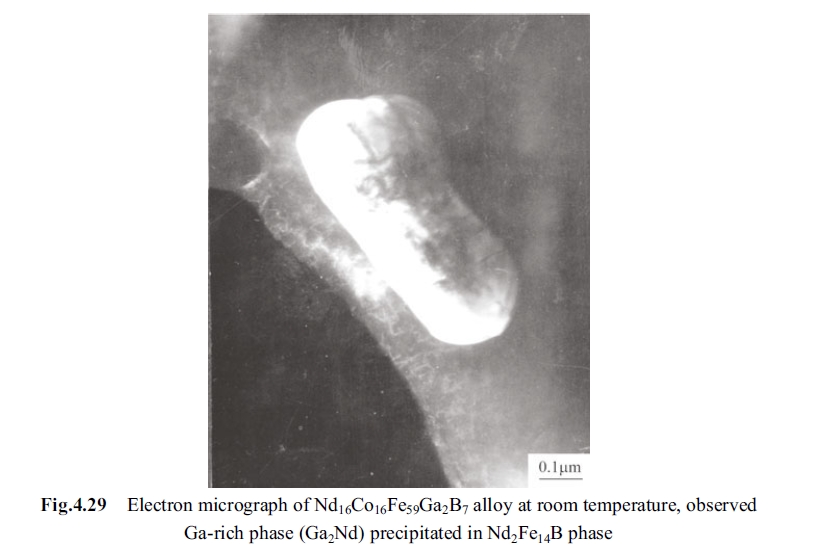

- Gallium is a non - magnetic atom and when it enters into the magnetic phase to form \(Nd_{2}(Fe,Ga)_{14}B\), it seems to have a magnetic dilution effect. Thus, the molecular magnetic torque is somewhat declined, the lattice constant \(c\) is increased, and the coercivity of the alloy is heightened.
Conclusions: Optimizing NdFeCoGaB Alloys for High-Temperature Magnetic Applications
NdCoFeGaB permanent magnetic alloy of high Curie temperature was prepared by means of powder metallurgy. Curie temperature of NdFeB permanent magnetic alloy was heightened from 312°C to 450 - 500°C; intrinsic coercivity of the alloy (\(_{i}H_{c}\)) reached to 716 - 955 kA/m, and magnetic energy product \((BH)_{max}=223 - 262\ kJ/m^{3}\). The study result using Mössbauer effect, etc. on sample of \(Nd_{16}Co_{16}Fe_{61 - x}Ga_{x}B_{7}\) indicated that when \(x = 2\) gallium atoms mainly occupy \(j_{2}\) site; when \(x>2\) gallium atoms also have a certain probability to occupy sites \(k_{2}\), \(j_{1}\), \(k_{1}\) besides \(j_{2}\). X - ray diffraction experiment attested to that for the tetragonal phase of this alloy the lattice constant \(a\) became the maximum at \(x = 2\) and the constant \(c\) increases with increase of \(x\) (from 1 to 7). The result of magnetic measurement found that the intrinsic coercivity presented a peak at \(x = 2\).






